空间最密堆积 | 开普勒猜想 | Mo's Notebook

学过晶体学的同学都知道，空间中球体的最密堆积是面心立方堆积 (FCC)和密排六方堆积 (HCP)。这似乎是毋庸置疑的。

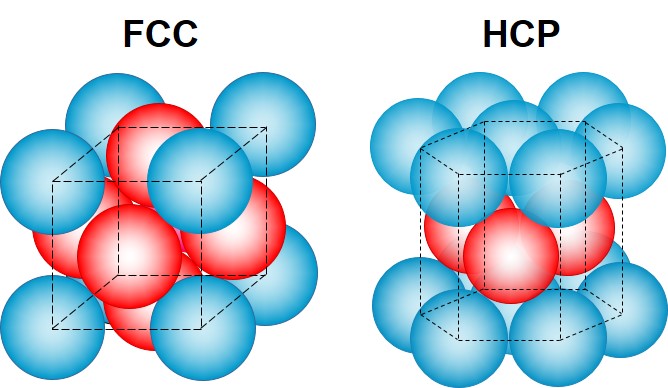
但是，大家有没有怀疑过为什么没有更多的最密堆积方法呢？

事实上这是一个古老的数学问题。其被命名为“开普勒猜想（Kepler Conjecture）”，这个猜想的内容是：没有任何其他的排列方式能够得到比面心立方堆积和密排六方堆积更大的平均空间利用率，同时这个最大的空间利用率大概是74.05%.

关于这段数学历史，知乎有一个挺有趣的回答。

1998年，Hales声称已经证明了这个猜想。这个证明方法是通过复杂的程序计算“穷举”了所有球体在空间中的排列方式。在后来的一段时间里，“开普勒猜想”已经被认为是一个公理。

直到2014年，Hales领导的Flyspeck团队称，使用Isabelle和HOL Light这两个辅助数学证明软件，正式证明了“开普勒猜想”。其全部代码已公开于GitHub（GitHub链接）。

其证明思路以Hales在2005年发表的一篇论文为基础。点击下方参考文献可下载原文。