从学术到工业 | 氧还原反应中的性能指标与实际燃料电池应用有何关系？

关键词：起始电位、极限扩散电流、燃料电池效率、燃料电池功率

写在前面

一如科研深似海。

这一方面是科学研究无边界的深度和广度所致，另一方面，也是由于我们自身思考的局限所致。

为什么这么说？

至少对国内的硕博士研究生来说，进入科研之后，我们就都面临着巨大的发文压力：满足毕业要求需要发文，评奖评优以发文为指标，在学术界生存那更是需要高质量的发文……久而久之，我们就都认识到了：文章（papers）是学术界的“硬通货”，与当今社会的一般等价物——货币，可以“相提并论”。

对于不擅长发文的同学们来说，其实还有另一条路可以选择——常常与学术界相对的工业界。

对大多数科研萌新来说，入门科研可能会经历以下历程（针对可工业化的科研方向）：

尝试理解文章逻辑->尝试理解测试指标->尝试掌握指标测试原理及方法->尝试理解其与工业产品指标的关系->优化产品设计

对工业界来说，创新性固然重要。但不同于学术界的任何意义上的创新，以实用为目的的创新，才是工业界真正急切需要的，也是目前中国所急切需要的。

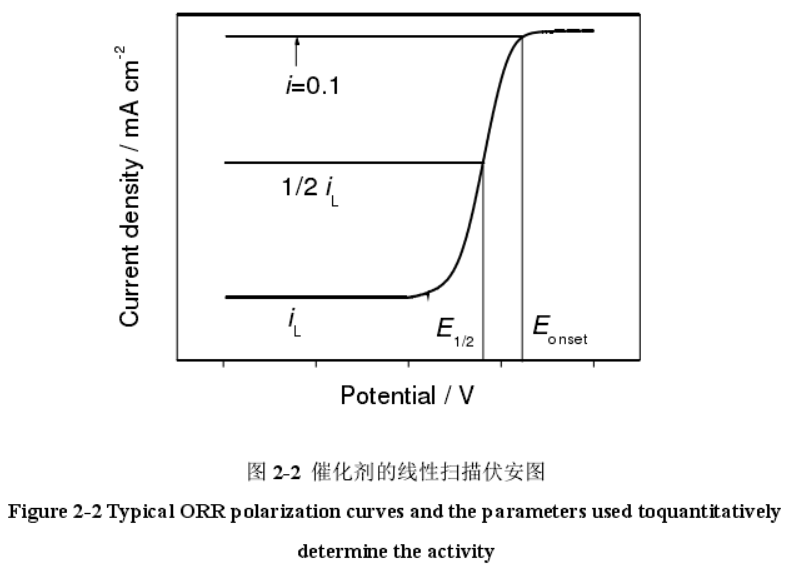
Ref: 周学俊. M-Nx/C类非贵金属氧还原催化材料的构筑及其电化学性能研究[D]. 东华大学, 2016.

笔者决定，针对自己的研究方向与目前研究热点，尝试讨论氧还原反应中极化曲线**起始电位（onset potential）**和**极限扩散电流密度（diffusion-limited current density）**所影响的燃料电池性能指标。希望能给各位从事新能源行业的新人们提供一些可以借鉴的思路。 # 起始电位与燃料电池效率 ## 如何理解起始电位 目前研究氧还原反应催化剂的文章中，起始电位（onset potential）是一个非常重要的指标。如果氧还原反应是一个**可逆**电化学反应，那么会有起始电位等于平衡电极电位 $$ E_{onset} = E_{eq} $$ 而平衡电极电位与反应的Gibbs自由能变化密切相关。如果有反应 $$ O_2 + 4H^++4e^- \to 2H_2O \quad 对应反应自由能变化\Delta G $$ 那么根据Gibbs自由能变化与平衡电极电势的关系有 $$ \Delta G = -nFE_{eq} $$ 即 $$ E_{eq} = -\frac{\Delta G}{nF} $$ 回到之前讨论的，燃料电池阴极上发生的氧还原反应比阳极上发生的燃料氧化反应慢好几个数量级，是一个不折不扣的**非可逆**电化学反应。如果将氧还原反应发生时所需过电势定义为 $$ \eta = |E_{onset} - E_{eq}| $$ 那么必须满足$\eta>0$且$E\_{onset}燃料电池内电势降分布示意图

Ref: Barbir F. PEM fuel cells: theory and practice[M]. Academic Press, 2012.

而事实上，自由能的一部分还会被燃料电池中的电势损耗消耗，如电化学极化、浓差极化等因素，所以一般地

$$ \Delta H = (W_{elec} + \int_{0}^{worktime} \eta I \text{d}t) + T \Delta S $$

上式中每一项均大于等于零，因此一般实际的燃料电池的效率在40%到60%之间。 # 极限扩散电流密度与燃料电池功率 在电极动力学足够快时，氧还原反应电流被氧气传质速率所控制。在氧气扩散速率达到最大时，此时对应电流成为极限扩散电流（diffusion-limited current）。 电极面积越大，便可以通过更大的电流。因此要研究材料本征性能，我们主要采用极限扩散电流密度（diffusion-limited current density）来描述材料的这类本征性能。 根据功率计算公式 $$ P = V \times I $$ 在燃料电池实际输出电压可以确定之后，其可输出的功率实际由其电流决定。电流越大，燃料电池可以输出的功率越大。 

Sources: https://www.nerdwallet.com/blog/loans/2016-toyota-mirai-fuel-cell-test-drive/

对新能源汽车应用来说，极限扩散电流密度越大，以一定功率为指标，我们的燃料电池电堆（相当于汽车内燃机发动机）便可以做得更小。

参考文献

[1] Barbir F. PEM fuel cells: theory and practice[M]. Academic Press, 2012.

[2] 周学俊. M-Nx/C类非贵金属氧还原催化材料的构筑及其电化学性能研究[D]. 东华大学, 2016.